
This study has shown that multiple methods used to quantitate the inhibition of drug efflux in a cell assay can result in different IC 50 values. The resulting IC 50 values varied according to the parameter evaluated, whether percent inhibition or percent control was applied, and the computational IC 50 equation. All three drugs decreased the secretory transport of digoxin in a concentration-dependent manner while increasing digoxin’s absorption to a lesser extent.
#GRAPHPAD PRISM 4 PARAMETER LOGISTIC CURVE SOFTWARE#
IC 50 values were then calculated using a variety of equations and software programs. From the permeability data, the efflux ratio and net secretory flux where calculated for each inhibitor. In a Caco-2 cell assay, the absorptive and secretive permeability of digoxin was measured in the presence of spironolactone, itraconazole and vardenafil. The objective of this study was to investigate variability in in vitro inhibition potency determination that may be due to calculation methods. Variability in in vitro parameter determination ( e.g., IC 50 values) among laboratories may lead to different conclusions in in vivo interaction predictions.
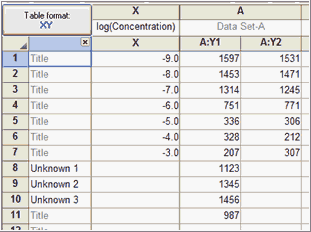
The potential for in vivo drug interactions is estimated through in vitro cell assays. You really don't have much data over an RFU of 150 which is just beyond the xmid value.Drug interactions due to efflux transporters may result in one drug increasing or decreasing the systemic exposure of a second drug. After graphing your data I would issue a warning about putting much confidence in the ending asymptote estimate. The A and B are obviously the starting and ending asymptotes. Model: RFU ~ SSfpl(Temperature, A, B, xmid, scal)Īchieved convergence tolerance: 1.541e-06 So it's as simple as ?SSfpl - to see the equation and supporting docs As such a self-starting version is already built into R in the form of the SSfpl function. The "Boltzmann sigmoid function" is exactly what Pinheiro and Bates call the "four parameter logistic function", since it's really just a rescaled version of the logistic function with different minima and maxima.

The Boltzmann sigmoid equation used by GraphPad PRISM software:įour-parameter Gompertz model used in G.4() function in R DRC library:į(x)=Y2+(Y1−Y2)exp(−exp(b(log(X)−e))). I need advice on the correct R library function. I am sure it is not the most appropriate choice. I selected G.4() function in the DRC package which was the closest self-starting model that was providing Tm values very close to the Boltzmann sigmoid function in PRISM. I am trying to predict melting temperature (Tm) values for the following sample data using the R DRC library function as shown below to mimic the calculation in GraphPad PRISM using Boltzmann sigmoid function.


 0 kommentar(er)
0 kommentar(er)
